MULTIPLICAR NÚMEROS MAYORES DE 5 CON LOS DEDOS.

Un recurso más, para aprender las tablas son las multiplicaciones de números mayores de cinco con las manos que, al fin y al cabo, son los resultados más dificultosos de recordar. Durante la Edad Media eran muy pocas personas las que conocían las tablas de multiplicar mayores de cinco. Se usaba un método muy popular que se basaba en el uso del complemento a 10 de los  números dados. El complemento de un número n respecto a 10 es 10-n. Por ejemplo, el complemento de 7 es 3. 

1. Numeración de los dedos.

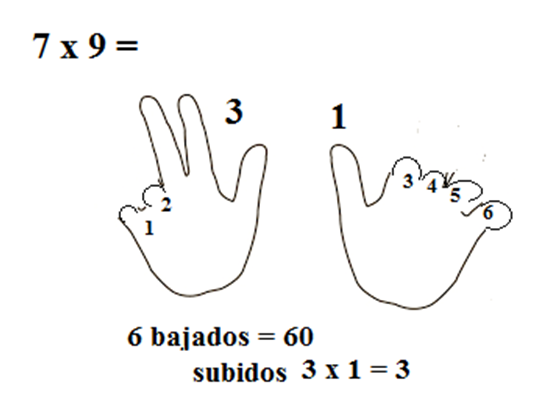
En primer lugar, como muestra la figura 1, se asocia a los dedos de cada mano los números 6,7, 8, 9 y 10, empezando por el dedo meñique. Como ejemplo que ilustra el método, vamos a hacer la multiplicación 7 por 9.

 - Para multiplicar 7 por 9, se doblan los dedos asociados (6 y 7 de la  mano izquierda y 6, 7, 8 y 9 de la mano derecha según figura 1). En figura 2 se observan doblados.

  Los cinco dedos bajados representan las decenas; en este caso, 6 decenas y los subidos se multiplican (figura  2).

- Luego 6 decenas son 60 unidades a las que se le suma el producto de los dedos levantados 3×1, es decir 3, dando un total de 60+3=63, que es el resultado.

Este método para multiplicar el producto de cualquier par de números comprendidos entre 6 y 10 fue muy usado durante el Renacimiento y hoy en día en ciertas zonas rurales de Europa y de Rusia.

 2. Multiplicación 7 x 9.

 Vamos a hacer otro ejemplo. Queremos multiplicar  6 por 7.

3. Multiplicación 6 x 7.

Tenemos tres dedos  doblados  (corresponde al 6 y al 6 y 7 de cada mano) que se suman y representan las decenas (figura 3).

- Tenemos 4 dedos extendidos en una mano y 3 en la otra. Dedos extendidos que se  multiplican y representan las unidades.

- Luego sumando  obtenemos el resultado de la multiplicación.

Podemos comprobar que es más difícil contarlo que hacerlo.

Este método facilita bastante el aprendizaje de las tablas pues los resultados de los números menores de 5 son siempre más asequibles para los alumnos.

Por si no te queda claro puedes ver este video donde se explica claramente..

Multiplicar con las manos - Bing video

PARA LOS MÁS CURIOSOS.

La explicación matemática sería la siguiente:

Al calcular p x q (p, q= 6, 7, 8, 9), se bajan p-5 dedos de la mano izquierda y se levantan 10-p dedos. En la mano derecha se bajan q-5 y se levantan 10-q dedos. Así pues, la suma de los dedos bajados de la mano izquierda con los dedos bajados de la mano derecha representan las decenas, es decir: 10(p-5+q-5). A este resultado se le suma el producto de los dedos que sobran de ambas manos es decir: (10-p)(10-q).

El  resultado final es:

10(p-5+q-5) + (10-p)(10-q) = 10p - 50 +10q - 50 + 100 + pq -10p-10q = pq 

Todo esto y más lo puedes encontrar en nuestra publicación

Barrantes, M., Zapata, M. y Barrantes, M.C. (2022). Didáctica de los números y las operaciones en la Educación Primaria. Ed. Universidad de Piura. Piura (Perú).

Y en nuestras entradas de este blog con la Etiqueta Números

 

¡CARNAVAL TE QUIERO!

El carnaval también es un tiempo importante para realizar actividades matemáticas sobre todo con los niños de infantil y primeros cursos.  Así, si los niños van disfrazados, sobre estos trajes, se pueden hacer observaciones y realizar conteos u operaciones de botones, círculos,  estrellas u otros objetos  que suelen aparecer en ellos.  

El maestro o maestra  también puede desarrollar la creatividad con algún disfraz matemático. Nos parece muy curioso este sencillo delantal o mandil, de la fotografía, en el que los bolsillos se utilizan para trabajar los números. Se introduce el símbolo numérico en un bolsillo  y en otro  los objetos equivalentes a dicho número, en dicha foto se hace con el número 3 y tres objetos. Abajo tiene un bolsillo  más grande para guardar los números y los objetos. Un disfraz fácil de hacer y útil matemáticamente hablando.  

Se pueden realizar también, en esta semana, fichas relacionadas con los números, las operaciones, las formas geométricas u otras materias, en las que esté presente el carnaval, como las que mostramos a continuación.  Son las mismas fichas de aprendizaje de los contenidos, pero utilizando la alegría y la ilusión que supone para los niños las fiestas de carnaval. 

¡FELIZ CARNAVAL MATEMÁTICO A TODOS!

GEOMETRÍA DE PAPEL.

Las actividades con papel son una gran ayuda en la educación geométrica. Este material proporciona al profesor desde los primeros cursos una herramienta pedagógica que le permite desarrollar diferentes contenidos, no sólo conceptuales sino de procedimiento. También desarrolla la psicomotricidad, fundamentalmente, la psicomotricidad fina, así como la percepción espacial.

La manipulación de papel desarrolla en el alumno la destreza manual, la exactitud en la realización del trabajo y la precisión manual. El manejo de papel, es una etapa esencial, fundamental e imprescindible para que los conceptos geométricos sean comprendidos y asimilados. Las actividades con papel se recomienda sean anteriores   a las actividades de construcción de figuras mediante el dibujo, pues para conseguir una mayor comprensión en el campo de la Geometría es preciso comenzar por la intuición que se ve reforzada con actividades tales como el doblado de papel.

Este material relaciona la Geometría  con otras ciencias y con las artes y, motiva al alumno a ser creativo, ya que puede desarrollar sus propios modelos e investigar la conexión que tiene con la Geometría no sólo plana, sino también espacial.

Igualmente que con otros recursos, el profesor tiene que posibilitar que los alumnos hagan sus descubrimientos, los comprueben y los comuniquen. Las fijaciones de los conocimientos y destrezas que se han experimentado y comprobado personalmente doblando papel serán mucho más duradera que aquellas que son de corte transmisivo.

Si seguimos el currículo de Primaria podemos observar que prácticamente todos los conceptos primarios se pueden trabajar con papel. En nuestro manual de didáctica de la Geometría podemos encontrar todo un apartado en el que se muestran más de cuarentas actividades, todas relacionadas con los programas oficiales de matemáticas. Después los alumnos pueden construir su propio cuaderno de Geometría de papel como el que mostramos en las fotografías.  

El  enlace del libro es el siguiente: 

(PDF) Geometría prohibido no tocar (researchgate.net)   

También se pueden encontrar esta actividades en:

Barrantes, M. y Barrantes, M.C. (2017). Geometría en la Educación Primaria. Ed. Indugrafic digital. Badajoz. Publicado en papel. Venta en librerías o ponerse en contacto con los autores: barrantes @unex.es

Presentamos una muestra de actividades que se pueden hacer para triángulos, que aparecen en los manuales. 

- Un triángulo cualquiera o un triángulo rectángulo son fáciles de construir.

- Un triángulo isósceles.Para construir un triángulo isósceles podemos considerar un rectángulo ABCD, podemos construir dos triángulos isósceles a partir de los vértices de un lado y el punto medio del lado opuesto, como se muestra en las figuras 1 y 2. Basta obtener mediante dobleces los ejes del rectángulo y unir los puntos indicados.

- Un triángulo equilátero (figura 3).  Tomamos una hoja rectangular y doblamos por la mitad paralelamente a los lados menores. Después doblamos uno de los vértices de modo que en la doblez, el vértice movido, en nuestro caso el B, se coloque sobre la doblez central. Marcamos ese punto como C, que será  el otro vértice del triángulo equilátero, y doblando CB obtenemos el otro lado, como se muestra en los dibujos. Llevar B sobre el eje central es equivalente a buscar el punto C que nos da la medida que iguala los segmentos AC y AB para que sea equilátero.

Otras actividades de investigación pueden ser:

- Cortando varios triángulos isósceles de ángulos iguales 30ª y desigual 120º.  Con tres de ellos se puede formar un triángulo equilátero. Estudiar que otras figuras se pueden formar.

- Cortar triángulos isósceles rectángulos iguales, con cuatro de ellos se puede formar un cuadrado. Estudiar qué otras figuras se pueden formar.

Los alumnos pueden probar propiedades como la comprobación de que “la suma de los ángulos de un triángulo miden dos rectos”. Se parte  del triángulo dado (figura 4), y doblando convenientemente los tres vértices A, B y C en el lado BC podemos observar que los tres vértices unidos nos dan dos rectos.

También aprovechando la figura anterior se puede probar que el área de un triángulo es la mitad del producto de la base por la altura (figura5)

 PARA LOS MÁS CURIOSOS

Johnson, D.A. y Wenninger, M.J. (1975). Matemáticas más fáciles con manualidades de papel. Barcelona. Distein ( libro antiguo pero imprescindible)

Revista  UNO Nº53 Monográfico dedicado a las Matemáticas y el papel.

TRIÁNGULO DE SIERPINSKI

El triángulo de Sierpinski es un fractal que aparece con frecuencia ya que hay muchas formas de generarlo. Lleva el nombre del matemático polaco Waclaw Sierpinski quién que lo introdujo en 1919 y  estudió sus propiedades matemáticas. Este fractal es construido a partir de encajar triángulos cada vez más pequeños en un triángulo equilátero como mostramos en las imágenes de abajo. 

Este modelo se ha utilizado como patrón decorativo durante siglos en catedrales y otros elementos. Aparece en la época medieval, a finales del siglo XII, cuando  una familia romana de artesanos del mármol:  Los Cosmati,  comenzaron a elaborar unos de los suelos más característicos de aquella época  en las iglesias de Roma  y  ciudades cercanas,  los llamados suelos  Cosmatescos. Encontramos diseños en Santa María la Mayor, Santa María Trastevere en Roma o  en la catedral de Rávena .

 Santa María 

 S. M. Trastevere

Entre las figuras aparecen triángulos de Sierpinski en rojo con pórfido y verde de  serpentina, incluso aunque no fuese un motivo original sino procedente de su restauración,  estos triángulos fueron  anteriores al nacimiento de Waclacw Sierpinski (1882-1969). Es decir, Sierpinski formalizó el modelo, pero este ya existía muchos años antes. 

En los centros escolares, también podemos trabajar dicho triángulo: hacer su construcción  y  colorearlo como vemos en las fichas de principio de esta entrega. 

El Triángulo también se puede construir en tres dimensiones, con lo cual tendríamos un tetraedro. Dicha construcción puede ser mediante ordenador con programas adecuados o manipulativamente como vemos en las fotos. Los tetraedros se unen mediante palillos de madera. 

En los siguientes videos mostramos como los alumnos de distintos institutos trabajan el Triángulo de Sierpinski con latas de refrescos. Son construcciones muy curiosas y vistosas. 

CONSTRUYENDO TRIÁNGULO DE SIERPINSKI CON LATAS RECICLADAS - Bing video

(28) Triángulo de Sierpinski en el IES Odiel - YouTube

(28) Triángulo de Sierpinski IES PINTOR PEDRO GÓMEZ (Huelva) - YouTube

PARA MÁS CURIOSOS

En nuestro libro Geometría ¡Prohibido no tocar! en el capítulo tercero presentamos un apartado sobre la Geometría y el arte.

https://www.researchgate.net/publication/349222640_Geometria_prohibido_no_tocar 

Para los que le gusten las manualidades mostramos este video de una construcción con papel  basada en el triángulo de Sierpinski. ¡Atrévete a hacerla!

Construyendo un fractal 1 Triángulo de Sierpinski - Bing video