BUSCANDO A PITÁGORAS : GEOMETRÍA DE PAPEL.

Las actividades con papel son una gran ayuda en la educación geométrica. Este material proporciona al profesor desde los primeros cursos una herramienta pedagógica que le permite desarrollar diferentes contenidos, no sólo conceptuales sino de procedimiento. También desarrolla la psicomotricidad, fundamentalmente, la psicomotricidad fina, así como la percepción espacial.

La manipulación de papel desarrolla en el alumno la destreza manual, la exactitud en la realización del trabajo y la precisión manual. El manejo de papel, es una etapa esencial, fundamental e imprescindible para que los conceptos geométricos sean comprendidos y asimilados. Las actividades con papel se recomienda sean anteriores a las actividades de construcción de figuras mediante el dibujo, pues para conseguir una mayor comprensión en el campo de la Geometría es preciso comenzar por la intuición que se ve reforzada con actividades tales como el doblado de papel.

Este material relaciona la Geometría con otras ciencias y con las artes y, motiva al alumno a ser creativo, ya que puede desarrollar sus propios modelos e investigar la conexión que tiene con la Geometría no sólo plana, sino también espacial.

Igualmente que con otros recursos, el profesor tiene que posibilitar que los alumnos hagan sus descubrimientos, los comprueben y los comuniquen. Las fijaciones de los conocimientos y destrezas que se han experimentado y comprobado personalmente doblando papel serán mucho más duradera que aquellas que son de corte transmisivo.

Si seguimos el currículo de Primaria podemos observar que prácticamente todos los conceptos primarios se pueden trabajar con papel. En nuestro manual de didáctica de la Geometría podemos encontrar todo un apartado en el que se muestran más de cuarentas actividades, todas relacionadas con los programas oficiales de matemáticas. Después los alumnos pueden construir su propio cuaderno de Geometría de papel como el que mostramos en las fotografías.

El enlace del libro es el siguiente:

(PDF) Geometría prohibido no tocar (researchgate.net)

También se pueden encontrar esta actividades en:

Barrantes, M. y Barrantes, M.C. (2017). Geometría en la Educación Primaria. Ed. Indugrafic digital. Badajoz. Publicado en papel. Venta en librerías o ponerse en contacto con los autores: barrantes @unex.es

Presentamos una muestra de actividades que se pueden hacer para triángulos, que aparecen en los manuales.

- Un triángulo cualquiera o un triángulo rectángulo son fáciles de construir.

- Un triángulo isósceles.Para construir un triángulo isósceles podemos considerar un rectángulo ABCD, podemos construir dos triángulos isósceles a partir de los vértices de un lado y el punto medio del lado opuesto, como se muestra en las figuras 1 y 2. Basta obtener mediante dobleces los ejes del rectángulo y unir los puntos indicados.

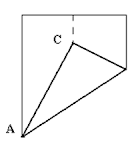
- Un triángulo equilátero (figura 3). Tomamos una hoja rectangular y doblamos por la mitad paralelamente a los lados menores. Después doblamos uno de los vértices de modo que en la doblez, el vértice movido, en nuestro caso el B, se coloque sobre la doblez central. Marcamos ese punto como C, que será el otro vértice del triángulo equilátero, y doblando CB obtenemos el otro lado, como se muestra en los dibujos. Llevar B sobre el eje central es equivalente a buscar el punto C que nos da la medida que iguala los segmentos AC y AB para que sea equilátero.

Otras actividades de investigación pueden ser:

- Cortando varios triángulos isósceles de ángulos iguales 30ª y desigual 120º. Con tres de ellos se puede formar un triángulo equilátero. Estudiar que otras figuras se pueden formar.

- Cortar triángulos isósceles rectángulos iguales, con cuatro de ellos se puede formar un cuadrado. Estudiar qué otras figuras se pueden formar.

Los alumnos pueden probar propiedades como la comprobación de que “la suma de los ángulos de un triángulo miden dos rectos”. Se parte del triángulo dado (figura 4), y doblando convenientemente los tres vértices A, B y C en el lado BC podemos observar que los tres vértices unidos nos dan dos rectos.