TAPAS DE ALCANTARILLAS

 

     

Buscando ejemplos para relacionar la geometría que se estudia en la Primaria con los objetos de la vida ordinaria, traemos hoy el de las tapas de alcantarillas. Nos preguntamos ¿porqué las tapas de las alcantarillas son redondas? La razón matemática es muy sencilla además de ser una razón de seguridad, pues estas tapas cierran agujeros de alcantarillas en las que los obreros tienen acceso. Así pues  lo importante es que no se nos caiga la tapa por el agujero.

 Para que la tapa no caiga, necesitamos una forma geométrica que tenga anchura constante que en los círculos es el diámetro. Esto implica, en nuestro caso, que si colocamos la tapa en el agujero de la alcantarilla, es imposible que dicha tapa entre por el agujero.

Si la tapa fuera cuadrada o rectangular entonces la anchura no es constante, ya que, por ejemplo, la distancia de la diagonal es mayor que cualquiera de los lados( por Pitágoras). Así pues,  la tapa cabe por el agujero si la metemos en diagonal, por lo que corremos el riesgo de que se nos caiga por él y cause algún accidente.  Si fuera cuadrada, un bromista podría sostener la cubierta en diagonal sobre el agujero y dejarla caer, para ser seguido por quién sabe cuántos  peatones.

        

Efectivamente podemos encontrar tapas cuadradas o rectangulares pero éstas se utilizan para tapar agujeros con muy poca profundidad, pues si no colocamos bien la tapa, o se nos resbala y se nos cae, podremos cogerla fácilmente. 

Explicada la razón podemos preguntarnos si hay otras formas que pueden ser utilizadas como tapas. La respuestas es Sí basta que cumplan la propiedad de anchura constante.  Así encontramos el triángulo de Reuleaux (ingeniero alemán que lo desarrolló) que es una curva de anchura constante basada en un triángulo equilátero. Este triángulo de Reuleaux es fácil de construir. Partimos de un triángulo equilátero y después trazamos tres circunferencias cuyo centro sea cada uno de los vértices y cuyo radio sea el lado del triángulo, como vemos en la figura.

         

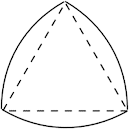
Así  tenemos otra figura, además del círculo, que cumplen que la anchura es constante. ¿Habrá en algún sitio tapas de alcantarilla con esta forma? Aquí tenemos unas tapas que se encuentra en San Francisco.

        

 Por último sería interesante hacer observar a los alumnos la cantidad de tapas que hay en los suelos de nuestras ciudades. Podrían estudiar la forma de cada una, así como la utilidad. 

Si te gusta el tema puedes mandarnos, en comentarios, fotografías de las tapas de tu ciudad. 

    

PARA LOS MÁS CURIOSOS.

Hay mucha literatura en internet sobre los polígonos de Reuleaux , que son polígonos de anchura constante, y sus aplicaciones en la vida ordinaria (monedas, taladradoras,..). Una muestra son los enlaces que adjuntamos.

Polígonos de Reuleaux | Mati, una profesora muy particular (20minutos.es)

Triángulos de Reuleaux y otras curvas de ancho constante | divulgadores.com