PORCENTAJES Y GRÁFICOS ¿NOS ENGAÑAN?

En los medios de comunicación nos invaden con porcentajes y gráficos para mostrarnos cualquier noticias. En estos días nos informaban de una manifestación que según la policía local habían asistidos 50. 000 personas y según la organizadora de la manifestación, 300.000 personas. Estos datos nos hacen pensar que hay  alguien no sabe contar bien. Pero hay otros ejemplos que no son tan claros y que el informado puede ser que no sepa observarlo.

 Empezamos por los porcentajes, que son muy  útiles cuando la población base es lo suficientemente grande para que expresar los datos en ellos. Sin embargo, en caso de valores base pequeños, sería mucho más exacto hablar en valores absolutos, lo que pasa es que mucha gente piensa que es mucho más formal y riguroso hablar en porcentajes. Da la impresión que dar un informe en valores absolutos no es serio. El ejemplo que añadimos nos aclara mucho.

Periódico matutino

 Los homicidios cometidos en la ciudad han aumentado un 60% con respecto al año anterior.

Da la impresión de que la inseguridad se ha apoderado de la ciudad. La realidad nos la da el periódico de la tarde.

Periódico vespertino

Los homicidios cometidos en la ciudad han aumentado de 5 a 8 con respecto al año pasado.

La moraleja nos indica que debemos enseñar a los alumnos a no confiar en los porcentajes cuando no se dan los valores base y que los porcentajes son desorientadores cuando las cifras bases son pequeñas.

Hacemos el ejercicio con los alumnos para comprobar que los dos resultados son el mismo. Se puede plantear  una regla de tres, si de 5 han aumentado 3, de 100 ¿Cuántos aumentan?  El resultado nos da los 60 buscados. O si de 5  homicidios pasamos a 8, de 100 ¿a cuántos homicidios pasamos? El resultado nos da 160 es decir un aumento de 60  cada 100.

Otro ejemplo de datos erróneos en los titulares de un periódico, que pueden causar una impresión errónea en los lectores, que no lean el artículo o no sean capaz de descubrir el error.

Según este articulo de El País, en el titulo de la noticia vemos Solo uno de cada seis parados cuenta con ayudas mientras que en la noticia, aparece el porcentaje de desempleado que recibe ayudas sobre el total de parados es del 61,28%, es decir 6 de cada 10 aproximadamente.

http://www.malaprensa.com/2013/06/error-y-rectificacion-en-el-pais.html

Lo mismo nos puede ocurrir con los gráficos.

Los gráficos son muy útiles, ya que nos ayudan a visualizar información compleja. En los tiempos que corren es muy  importante enseñar a los alumnos la interpretación de gráficos.  Pero éstos también son peligrosos: tendemos a creernos más la información que se presenta de forma visual que de forma escrita, ya que nos da la impresión de ser más objetiva. Es decir, a menudo olvidamos que esta información visual puede contener errores y, por supuesto, ser tendenciosa.

Hay una serie de prácticas que nos deben alertar si las vemos en un gráfico. No quiere decir que los gráficos que usen estas técnicas estén mal hechos, pero sí que merece la pena mostrar algo de precaución y sentido crítico porque es posible que estén jugando con nuestra percepción de los datos. En el siguiente ejemplo (Paro 2013) al no estar marcado el eje vertical, da impresión de  que se produce una gran bajada del paro, cuando los datos numéricos  no son significativamente tan distintos.

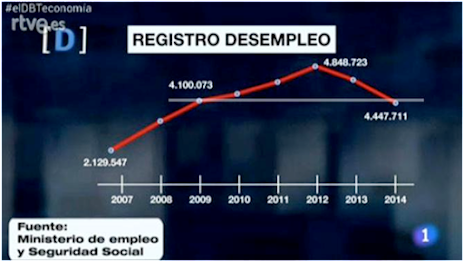
En el segundo ejemplo (Registro desempleo), tampoco está marcado el eje vertical, el lector puede observar que se comete un error al colocar a la misma altura dos valores distintos.

 Hay que tener, también, cuidado en los gráficos y diagramas de sectores (tartas), sobretodo,  en tres dimensiones son muchos más útiles para suministrar informaciones tendenciosas.

En este diagrama de sectores se puede ver la desproporción  del espacio ocupado entre cuatro ediles y 3 ediles claramente con una realización mal intencionada. Se observa mejor, observando el espacio ocupado por los 7 primeros ediles en comparación a los 6 últimos. Además estos últimos no se sabe de qué partido son. Veamos un ejemplo, ya antiguo pero clásico, dentro de las imprecisiones que se pueden cometer en el uso de diagramas de tres dimensiones.   

Claramente la diferencia de los cilindros es significativa visualmente pero no numéricamente, además la escala del cilindro no está graduada ni comienza desde cero.

Concluimos diciendo que  los alumnos como ciudadanos deben tener capacidad para leer y comprender las informaciones, y una vez comprendida aceptarla o rechazarla de una manera consciente y personal. Comprender la información no significa solamente comprender una idea o una tendencia, sino tener capacidad para  reinterpretar la que viene expresada en términos matemáticos o la que se genera a partir de números, porcentajes o gráficos.

Es necesario que los profesores enseñen a los alumnos a interpretar correctamente los gráficos con los que son bombardeados diariamente y sepan leerlos correctamente descubriendo las imprecisiones que pueden tener. Es evidente que en caso contrario la manipulación a la que el ciudadano medio puede ser sometido mediante la información numérica no tiene límite.

Queremos formar ciudadanos libres y críticos pero no manipulados.