Las
actividades con papel son una gran ayuda en la educación geométrica. Este
material proporciona al profesor desde los primeros cursos una herramienta
pedagógica que le permite desarrollar diferentes contenidos, no sólo
conceptuales sino de procedimiento. También desarrolla la psicomotricidad,
fundamentalmente, la psicomotricidad fina, así como la percepción espacial.
La
manipulación de papel desarrolla en el alumno la destreza manual, la exactitud
en la realización del trabajo y la precisión manual. El manejo de papel, es una
etapa esencial, fundamental e imprescindible para que los conceptos geométricos
sean comprendidos y asimilados. Las actividades con papel se recomienda sean
anteriores a las actividades de construcción de figuras
mediante el dibujo, pues para conseguir una mayor comprensión en el campo de la
Geometría es preciso comenzar por la intuición que se ve reforzada con
actividades tales como el doblado de papel.
Si
seguimos el currículo de Primaria podemos observar que prácticamente todos los
conceptos primarios se pueden trabajar con papel.
El
alumno solamente necesita: papeles necesarios para realizar los ejercicios y
rotuladores; a nosotros nos gusta trabajar con cuartillas (cuarta parte de un
A4). Es importante que las rectas, puntos, etc. sean señalados suficientemente
para que pueda ser visto por la cara de detrás y por ello, se recomienda a los
alumnos dibujar con rotuladores Esto
ayuda bastante a la hora de doblar y obtener el resultado buscado. En otra
entrega (5-2-21) vimos cómo construir todo tipo de triángulos mediante doblado
de papel, por eso hoy nos vamos a describir como doblar las figuras de más de
tres lados que estudiamos en la enseñanza escolar.
Desarrollamos
actividades para los alumnos de Primaria y también, para los estudiantes para profesores o profesores.
1)
Actividades para los alumnos de Primaria. Cuadriláteros
Construir:
1- El cuadrado. El primer cuadrilátero que construimos es el cuadrado. Podemos hacerlo mediante un nudo con dos tiras de igual anchura, como se ve en la figura 1 y suprimiendo con una tijera el trozo restante.
Figura 1. Construcción de un
cuadrado con tiras de papel
También se puede hacer mediante un
trozo de papel rectangular: llevando el lado más pequeño sobre el mayor, nos da
la medida del lado, cortando el resto sobrante de rectángulo, obtenemos el
cuadrado.
2.
Un
rombo. Podemos construir un rombo a partir de un rectángulo.
Basta con hallar los puntos medios de los lados y unirlos mediante dobleces (figura
2).
Actividades
para estudiantes para profesores o profesores.
- Cortando un cuadrado por sus diagonales que otras figuras planas se pueden conseguir. Clasifíquelas. ¿Qué tienen todas en común, además de ser figuras planas?
Figura 2. Construcción de un rombo
doblando papel.
- Igualmente cortando un rectángulo por una diagonal.
- Diseña una forma de construir un rectángulo y un
paralelogramo doblando papel
- Calcular el área del paralelogramo a partir del área de un
rectángulo doblando papel y si lo
necesitas recortando.
- Comprobar doblando, que el punto de corte de las diagonales del paralelogramo es
equidistante de los vértices. Ídem cuadrado, rombo y rectángulo ¿en qué casos
son iguales en longitud?
c)
Actividades para los alumnos. Trapecios.
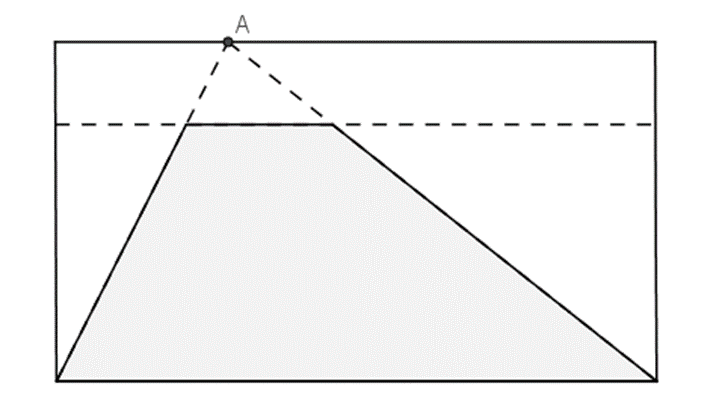
Figura 3.Construcción de un trapecio
doblando papel.
La construcción de un trapecio es
sencilla. Para ello, tomamos un rectángulo, vale un A4 o cuartilla, y sobre uno de sus lados marcamos un punto A
cualquiera. Trazamos dos segmentos
(dobleces) desde los vértices del lado opuesto hasta el punto A.
Trazando una paralela al lado que contiene a A, obtenemos el trapecio, como vemos
en la figura 3.
Actividad
para estudiantes para profesores.
- ¿Qué condición debe cumplir el
punto A para que el trapecio nos salga isósceles? ¿y para que nos salga
trapecio rectángulo?
d)
Actividades para los alumnos. Figuras de más de cuatro lados doblando papel.
Construir:
1- El pentágono. Es
un figura que se puede conseguir mediante doblado de papel pero su construcción
no la consideramos adecuada para la Primaria por la dificultad que
entraña, por lo que nos limitaremos a
mostrar un pentágono de papel que se construye con una tira haciendo en ella, simplemente,
un nudo (Figura 4.)
Figura 4. Construcción de un
pentágono regular mediante un nudo.
El
alumno puede comprobar midiendo los lados que el pentágono que nos sale es totalmente regular.
2-
El
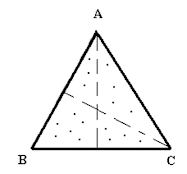
exágono regular. Es sencillo de
construir pues para ello nos basta con tomar un
triángulo equilátero y obtener su centro (por ejemplo, trazando dos alturas,
figura 5). Si doblamos los vértices del triángulo de modo que coincidan en el
centro, obtenemos el exágono regular. Los alumnos pueden comprobar que es
regular midiendo sus ángulos, sus lados,…
También se puede conseguir el hexágono, el heptágono o el octógono mediante un nudo de dos cintas de igual anchura - pero consideramos que estás formas, por su complicación, son apropiadas para cursos superiores a los de la Primaria (como se pueden ver en: Donovan, A. J. y Magnus, J.W.: Matemáticas más fáciles con manualidades de papel. Barcelona: Vanguardia pedagógica Distein, 1975).
Actividad
para estudiantes para profesores.
- Partiendo de un exágono regular, dibujado en un papel, construye un dodecágono regular mediante dobleces.

Figura 5. Construcción del exágono regular doblando papel.
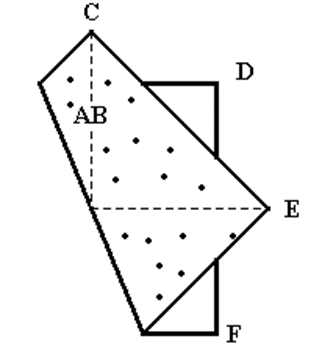
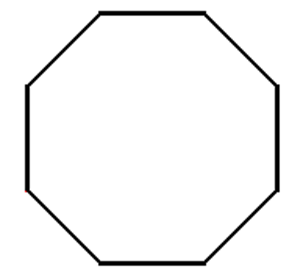
3- El octógono. Puede ser obtenido por los alumnos
a partir de un cuadrado. En primer lugar,
trazamos (doblando) todos los ejes de simetrías del cuadrado. El siguiente paso
es hacer coincidir dos de los ejes (A y B) y una vez hecho esto, podemos
observar que nos quedan cuatro vértices no solapados (C, D, E, F ). Sin desdoblar la coincidencia de ejes, doblamos
los cuatro vértices, siempre hacía la cara posterior. Hecho esto, ya podemos
desdoblar y obtener el octógono como se muestra en la figura 6.
Figura 6. Construcción de un octógono regular doblando papel.
-
Otra
forma de trazar un octógono. Se parte de un cuadrado en el que calculamos,
doblando, los puntos medios de sus lado GEFH. Con estos puntos de vértices trazamos
el cuadrado correspondiente (en
el dibujo en línea discontinua). Ahora trazamos las bisectrices de los ángulos
(líneas más gruesas) que forman los lados
del cuadrado GEFH con los lados de ABCD,
por ejemplo, vértice E y lados EA y EG.
Trazados dichas bisectrices y unidas de dos en dos se obtiene el octógono que vemos en la figura
7 en línea gruesa. El alumno puede observar, en los dos casos, que los
octógonos obtenidos son regulares.

Figura 7. Construcción de un
octógono regular mediante dobleces.
PARA LOS
MÁS CURIOSOS
En nuestro
manual, puede encontrar más actividades de doblado de papel.
Barrantes, M., Barrantes, M.C.
(2021).Geometría ¡prohibido no tocar! Universidad de Extremadura, Servicio de
Publicaciones. Badajoz
(PDF)
Geometría prohibido no tocar (researchgate.net)